Découverte de Geogebra (11H)
Descriptif
Cycle
11e année, Cycle 3
Discipline(s) d'enseignement
- Mathématiques
Référence(s) au PER
Progressions des apprentissages PER EdNum
Les progressions des apprentissages PER EdNum seront publiées prochainement.
Sous-objectif(s) MITIC: l'élève est capable de...
- 3A.2 - Choisir les ressources numériques (texte, présentation, feuille de calcul, dessin, musique, etc.) en fonction de la tâche à accomplir.
Références au(x) moyen(s) d'enseignement
Mathématiques 9-10-11, Livre 11e

Déroulement
| Organisation | Déroulement / Etapes | Moyens |
|---|---|---|
| 5' C | L’enseignant-e présente brièvement le mode de fonctionnement du logiciel : l’affichage, la sélection d’un outil, comment effacer un objet créé,… et laisse les élèves découvrir librement le logiciel. | Logiciel Geogebra |
| 35' E | Distribution de la fiche de travail. Les élèves prennent une page blanche (Fichier -> Nouveau) et suivent le pas-à-pas pour réaliser la construction géométrique (partie A). Interprétation de la construction produite (Parties B et C): Les élèves complètent le tableau. Le but est de montrer que la construction permet de déterminer la fonction y = sqrt{x} | Logiciel Geogebra Document de l'élève |
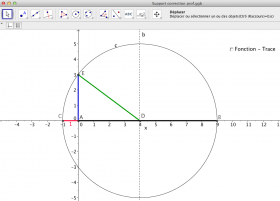
| 10' C | Correction : à l’aide du fichier «Support correction pour l'enseignant-e». L’enseignant-e montre la construction correcte et peut aisément tracer la fonction en activant la trace active du point de coordonnées (x ; sqrt{x} ) (Utiliser la case à cocher pour faire afficher ou non ce point). | Support de correction pour l'enseignant-e (fichier GeoGebra) |
Organisation : C = toute la classe G = groupe E = travail individuel DC = demi-classe L = libre HC = hors-classe
Remarques
Les élèves (plutôt PG) peuvent démontrer algébriquement que cette construction permet de trouver la racine carrée d'un nombre. Ils utilisent pour ce faire le théorème de Pythagore.